[PRX 7:011014, 2017]
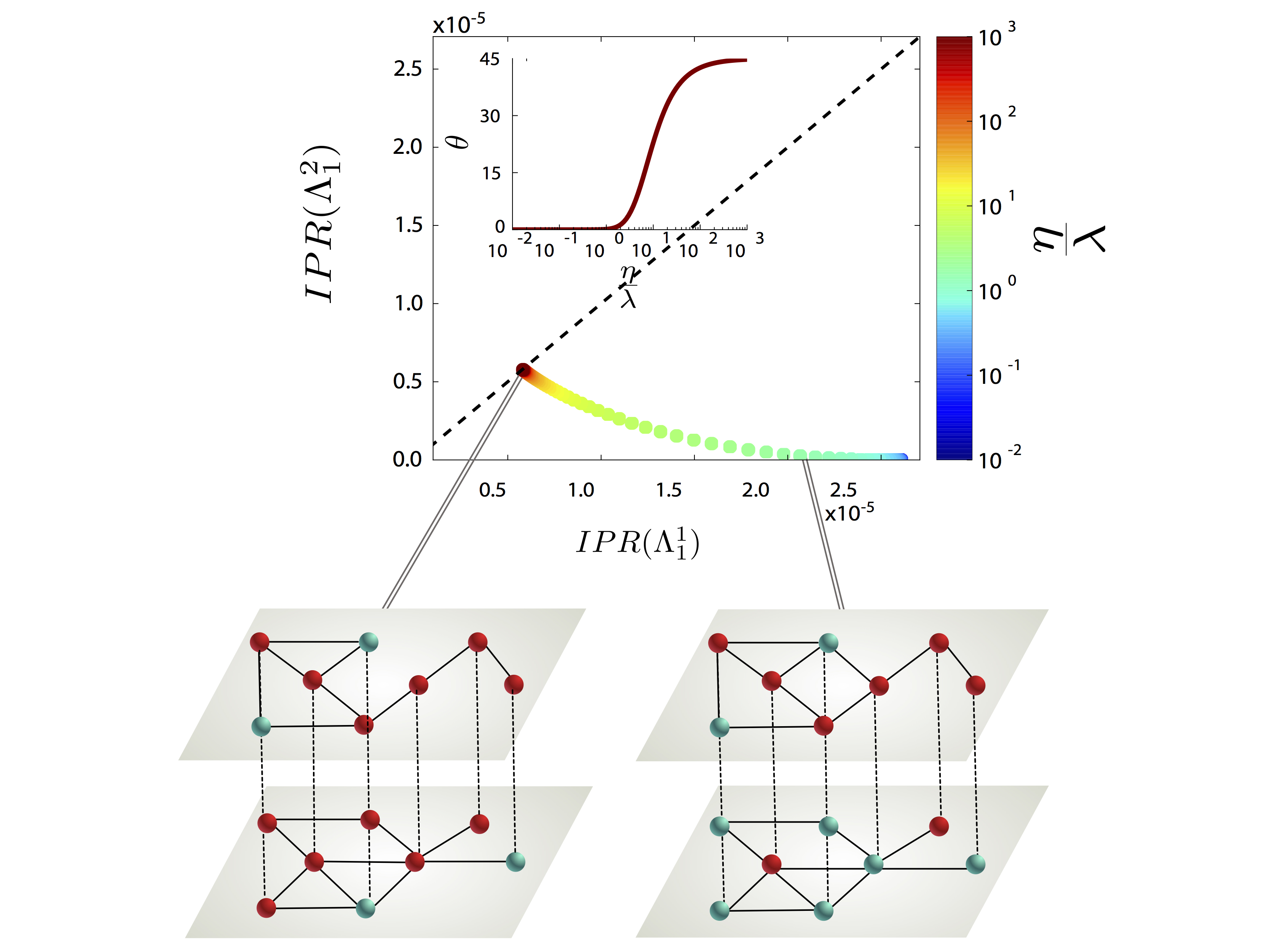
Disease Localization in Multilayer Networks.

We present a continuous formulation of epidemic spreading on multilayer networks using a tensorial representation, extending the models of monoplex networks to this context. We derive analytical expressions for the epidemic threshold of the susceptible-infected-susceptible (SIS) and susceptible- infected-recovered dynamics, as well as upper and lower bounds for the disease prevalence in the steady state for the SIS scenario. Using the quasistationary state method, we numerically show the existence of disease localization and the emergence of two or more susceptibility peaks, which are characterized analytically and numerically through the inverse participation ratio. At variance with what is observed in single-layer networks, we show that disease localization takes place on the layers and not on the nodes of a given layer. Furthermore, when mapping the critical dynamics to an eigenvalue problem, we observe a characteristic transition in the eigenvalue spectra of the supra-contact tensor as a function of the ratio of two spreading rates: If the rate at which the disease spreads within a layer is comparable to the spreading rate across layers, the individual spectra of each layer merge with the coupling between layers. Finally, we report on an interesting phenomenon, the barrier effect; i.e., for a three-layer configuration, when the layer with the lowest eigenvalue is located at the center of the line, it can effectively act as a barrier to the disease. The formalism introduced here provides a unifying mathematical approach to disease contagion in multiplex systems, opening new possibilities for the study of spreading processes.
G. Ferraz de Arruda, E. Cozzo, T. P. Peixoto, F. A. Rodrigues, and Y. Moreno, “Disease Localization in Multilayer Networks”, Physical Review X 7, 011014 (2017).
Multi-scale Diseases
[PRX 4:041005, 2014; Plos Comp. Biol. 9:e1003169, 2013]
Current modeling of infectious diseases allows for the study of complex and realistic scenarios that go from the population to the individual level of description.
The advances in the realism of epidemic modeling are however hampered by our current limitations to properly deal with several factors such as:
real demographic distributions, detailed migration and mobility patterns, human behavioral responses to the presence of an outbreak, disease’s multi-strain, and the concurrency of several diseases, among others.
Most epidemic models assume that the spreading process takes place on a single level
(be it a single population, a meta-population system or a network of contacts). The latter results from our current limited knowledge about the interplay among the various scales involved in the transmission of infectious diseases at the global scale. Therefore, pressing problems rooted at the interdependency of multi-scales call for the development of a whole new set of theoretical and simulation approaches. It is extremely importatnt to develop disease-specific theoretical and computational models to understand the transmission mechanisms behind global public health threats. The fact of considering the interdependency between many levels and scales represents a radical change that makes a substantial difference as it allows addressing problems such as comorbidity and the spreading of persistent infections and multi-strain diseases. Thus, the goal consists of developing a contemporary epidemiological framework that integrates the many aspects involved in the spreading of global diseases: from single networks of contacts to meta-population systems and from the interaction between different diseases and strains to the influence of human behavioral changes and mobility patterns.
Interacting Diseases
The description of the evolution of a single disease on a particular network of contacts has been the subject of intense research during the last several years. Nowadays, we have a set of tools that allows addressing the previous challenge to a large degree of details. However, in many situations, multiple pathogens coexist within the same host population and usually interact among each other. This includes, for example, systems of competing pathogens (e.g., seasonal influenza) or the so-called syndemic systems (e.g. HIV and Tuberculosis), i.e., two pathogens each of which enhances or impairs the spreading of the other.

In this paper, we develop a theoretical and computational framework to study the dynamics of concurrent diseases. We propose a model for the description of the simultaneous spreading of two interacting pathogens on the same host population through independent contact networks. The model is based on an heterogenous mean-field approach to describe the critical properties of the dynamics as well as an adequate framework for the temporal description of coupled out of equilibrium outbreaks for both the Susceptible-Infected-Susceptible and Susceptible-Infected-Removed scenarios. The proposed framework allows to analytically derive the epidemic thresholds of the diseases modeled, explicitly addressing the influence on each threshold on aspects such as the prevalence of the conjugate disease, the system size, the architecture of the networks of contacts and the appearance of eventual correlations between them.
Overall, our findings provide deep insights into what are the key mechanisms that drive the evolution of interacting diseases and secondly, they pave the way for the development of quantitative, data-driven models for the detailed characterization of concurrent and interacting diseases.
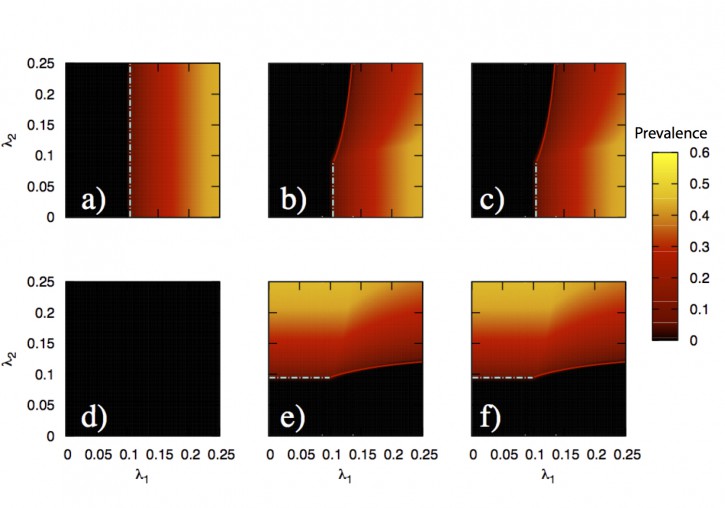
J. Sanz, C.-Y. Xia, S. Meloni and Y. Moreno, “Dynamics of interacting diseases”, Physical Review X 4, 041005 (2014).
Human Behavioral Changes
The inclusion of mobility processes is a key ingredient in the modeling of the geographic spread of epidemics. Models that explicitly take into account the mobility patterns of individuals range from relatively coarse-grained approaches that consider aggregated traveling flows to highly detailed structured meta-population or agent-based models allowing for the description of billions of individuals.
However, the available data on human mobility and interaction are descriptive of human behavior as long as information concerning the unfolding of the epidemic does not induce changes in the population’s behavior, for at this point the model has to include the population’s behavioral changes that in turn alter the epidemic spreading.
In particular, self-initiated behavioral changes are elusive to modeling because of the difficulty involved in quantifying these changes and an overall lack of relevant data. Although there have been some attempts to develop formal models, only a few of these theoretical and computational approaches have considered the spatially structured nature of populations. Therefore, the effect of behavioral and mobility changes in the large-scale spreading of the epidemic is still an open problem. It is thus of utmost importance to further investigate into this issue.
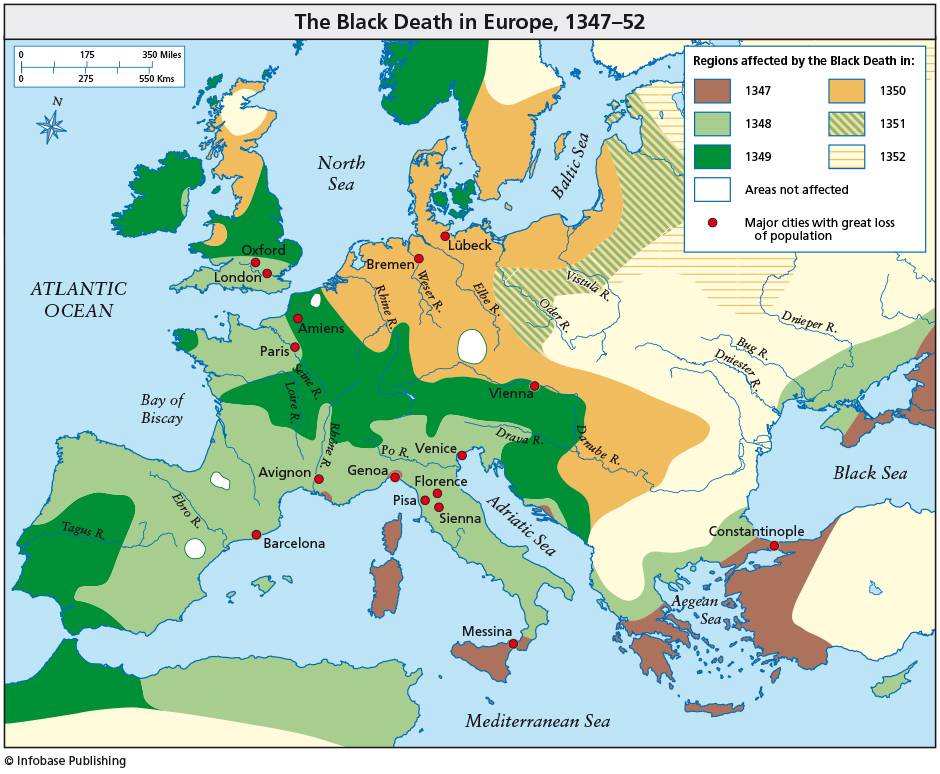
Black Death came to Europe in 1347 (Messina, Sicily) and it took about 4 years to spread throughout the European continent. This devastating plague began in Asia and spread westward along trade routes. The pandemic killed millions of people and its progress was gradual. About one-third of the entire population of Europe might have died. Nowadays, an epidemic can spread all over the world in just a few days or maybe hours. In this sense, globalization thanks to air transport plays a crucial and decisive role.
S. Meloni, N. Perra, A. Arenas, S. Gomez, Y. Moreno, and A. Vespignani, “Modeling Human Mobility Responses to the Large-scale Spreading of Infectious Diseases”, Scientific Reports 1, 62 (2011).
Multi-strain Epidemics
Current state-of-the-art epidemiological models incorporating complex patterns of interactions (no matter whether at the level of meta-populations or not) are devised to deal with a single spreading process, i.e., they are not thought to deal with situations in which several strains of the same disease coexist.
These models are most needed to study complex disease contagion. In an increasingly globalized world, in which population movements are becoming more frequent and massive, we must realize that what happens anywhere in the world has an impact on our environment. It is therefore the time to develop models that address the effects of the interaction between multiple strains in structured populations. Their integration into current theoretical and modeling efforts to aid our understanding of the mechanisms of transmission and evaluation of potential control strategies constitutes one of the main goals.
To study the dynamics of multi-strain epidemics, one has to extend the traditional framework to consider multiple strains of a disease spreading through one host species. This kind of models is in its early infancy, as the scientific community is only starting to understand the wide spectrum of complex outcomes that result from the competition of multiple strains for a limited number of susceptible individuals in unstructured populations. The need to address the issue of multiple strains’ interactions is becoming increasingly recognized as one of the most fundamental open problems in modern epidemiology and public health.
C. Poletto, S. Meloni, V. Colizza, Y. Moreno and A. Vespignani, “Host mobility drives pathogen competition in spatially structured populations”, PLoS Computational Biology 9 (8): e1003169 (2013).
C. Poletto, S. Meloni, A. Van Metre, V. Colizza, Y. Moreno and A. Vespignani, “Characterizing two-pathogen competition in spatially structured environments”, Scientific Reports 5:7895 (2015).
Individual-Level and Meta Population Approaches
The critical properties of an epidemic outbreak in complex networks were first addressed using the heterogeneous mean-field (HMF) prescription. This framework has been proved to be exact in annealed networks, whose nodes’ degrees are sampled from a fixed degree distribution at each step of the dynamics (i.e. its specific connectivity is fixed only in average).
However, in specific realizations of a model’s topology (
quenched networks), HMF can result in different levels of accuracy. This problem leads to the question of whether or not the direct use of the HMF approach is accurate enough when dealing with real networks. On the other hand, meta-population approaches are an essential theoretical framework used in Epidemiology, population ecology, genetics and adaptive evolution to describe population dynamics whenever the spatial structure of populations plays an important role in the system’s evolution.
The basic assumption of meta-population models is that the system under study is highly fragmented and characterized by populations localized in relatively isolated discrete units/subpopulations connected by some degree of migration and or commuting. Two different dynamics take place concurrently: inside each subpopulation and between subpopulations. The most important difference with respect to single population models is the existence of a second epidemic threshold. This new critical point, known as global invasion threshold, marks the point beyond which a local outbreak reaches other subpopulations and spreads throughout the meta-population system. The global invasion point does not only depend on the infection parameters, but also on the mobility rates of individuals as well and thus differs from the single population epidemic threshold.
Recent works have extensively applied meta-population schemes to understand the epidemic dynamics of spatially structured populations. However, theoretical approaches are all at the mean-field level and use a tree-like approximation that represents the evolution of the number of diseased subpopulations as a branching process. In addition, individuals within the subpopulations are all well mixed and no sources of heterogeneity (neither in the networks of contacts nor in the individual mobility rates) at the lower individual scale are built in the models. Finally, data-driven computations are very intensive and lengthy, especially when modeling disease propagation worldwide. We therefore aim at integrating individual-level approaches into meta-population schemes to add further realism to the structure of subpopulations.
© June 2013, COSNET Lab · BIFI, Zaragoza, Spain. All rights reserved.
 [PRX 7:011014, 2017]
[PRX 7:011014, 2017]





