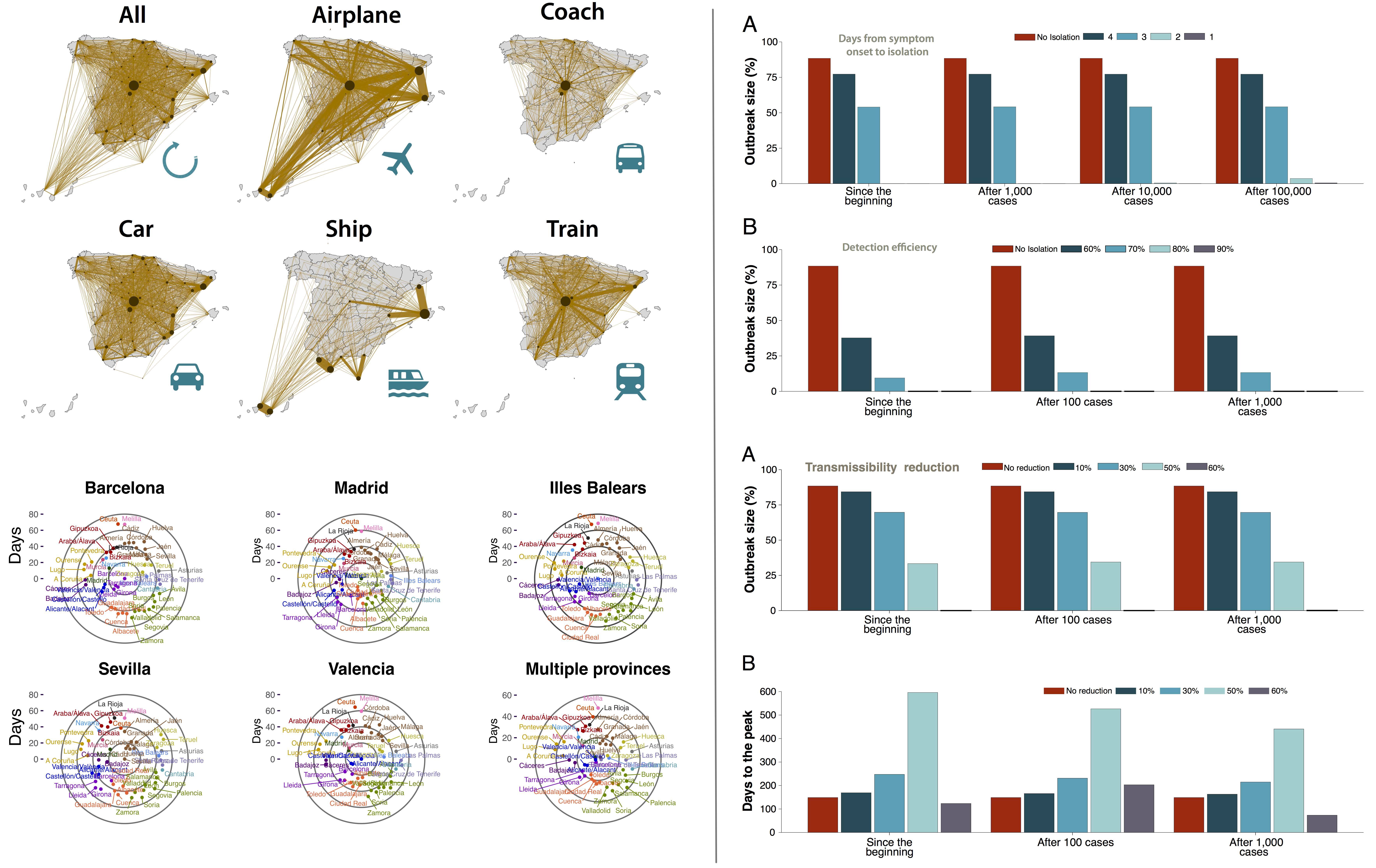
Summary:
Background: We are currently experiencing an unprecedented challenge, managing and containing an outbreak of a new coronavirus disease known as COVID-19. While China—where the outbreak started—seems to have been able to contain the growth of the epidemic, different outbreaks are nowadays present in multiple countries. Nonetheless, authorities have taken action and implemented containment measures, even if not everything is known.
Methods: To facilitate this task, we have studied the effect of different containment strategies that can be put into effect. Our work referred initially to the situation in Spain as of February 28, 2020, where a few dozens of cases had been detected but it has been updated to match the current situation as of 13 April. We implemented an SEIR metapopulation model that allows tracing explicitly the spatial spread of the disease through data-driven stochastic simulations.
Results: Our results are in line with the most recent recommendations from the World Health Organization, namely, that the best strategy is the early detection and isolation of individuals with symptoms, followed by interventions and public recommendations aimed at reducing the transmissibility of the disease, which, although might not be sufficient for disease eradication, would produce as a second-order effect a delay of several days in the raise of the number of infected cases.
Conclusions: Many quantitative aspects of the natural history of the disease are still unknown, such as the amount of possible asymptomatic spreading or the role of age in both the susceptibility and mortality of the disease. However, preparedness plans and mitigation interventions should be ready for quick and efficacious deployment globally. The scenarios evaluated here through data-driven simulations indicate that measures aimed at reducing individuals’ flow are much less effective than others intended for early case identification and isolation. Therefore, resources should be directed towards detecting as many and as fast as possible the new cases and isolate them.

Alberto Aleta, and Yamir Moreno, “Evaluation of the potential incidence of COVID-19 and effectiveness of contention measures in Spain: a data-driven approach”, BMC Medicine 18:157 (2020).
Summary:
This book provides the basis of a formal language and explores its possibilities in the characterization of multiplex networks. Armed with the formalism developed, the authors define structural metrics for multiplex networks. A methodology to generalize monoplex structural metrics to multiplex networks is also presented so that the reader will be able to generalize other metrics of interest in a systematic way. Therefore, this book will serve as a guide for the theoretical development of new multiplex metrics. Furthermore, this Brief describes the spectral properties of these networks in relation to concepts from algebraic graph theory and the theory of matrix polynomials. The text is rounded off by analyzing the different structural transitions present in multiplex systems as well as by a brief overview of some representative dynamical processes. Multiplex Networks will appeal to students, researchers, and professionals within the fields of network science, graph theory, and data science.
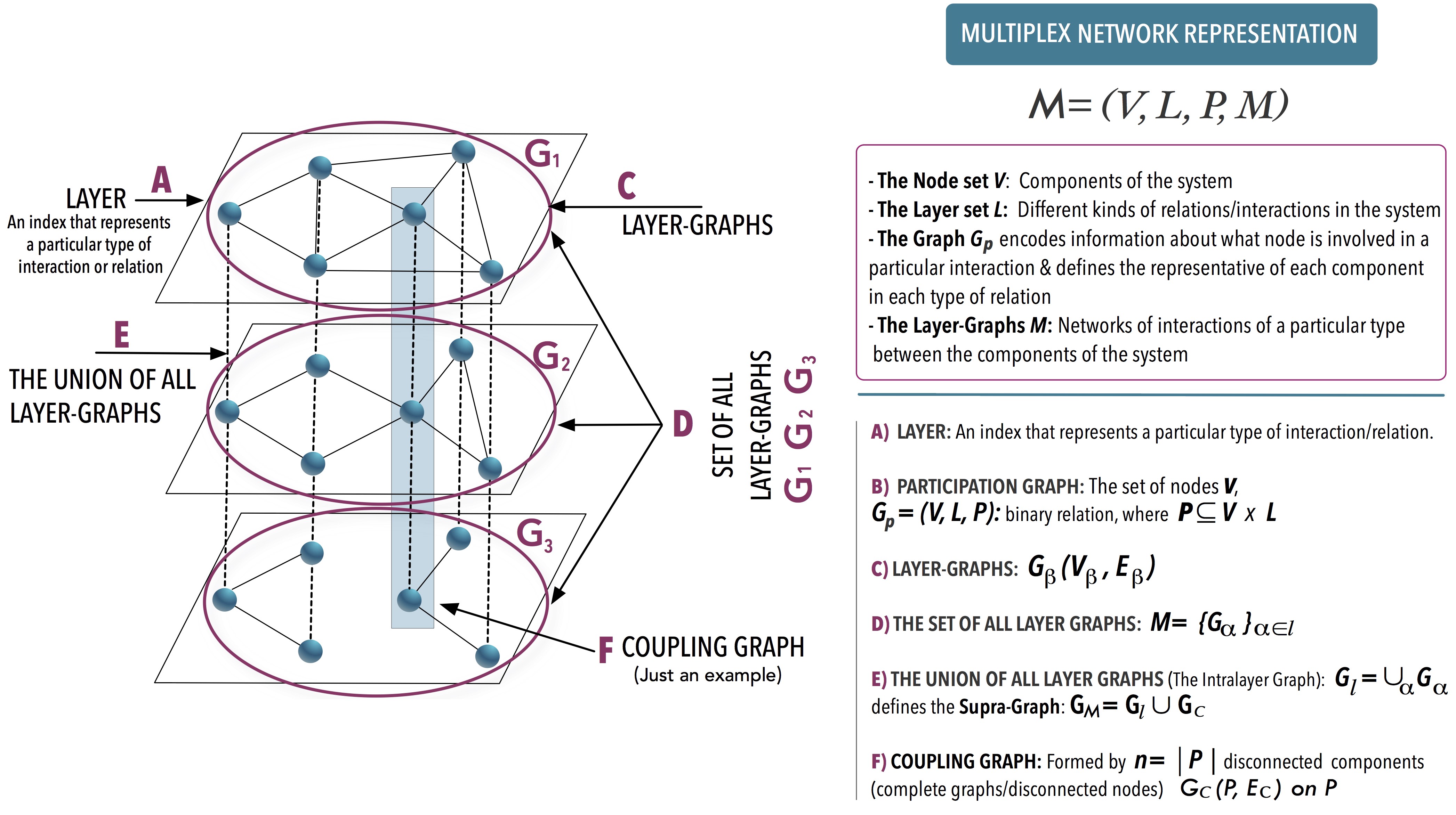
E. Cozzo, G. Ferraz de Arruda, F. A. Rodrigues, and Y. Moreno, “Multiplex Networks: Basic Formalism and Structural Properties”, Monograph Springer Briefs in Complexity, ISBN 978-3-319-92255-3 (2018).
[PNAS 115, E3238-E3245 (2018).]Data-driven model of Tuberculosis Spreading
In the case of tuberculosis (TB), the capabilities of epidemic models to produce quantitatively robust forecasts are limited by multiple hindrances. Among these, understanding the complex relationship between disease epidemiology and populations’ age structure has been highlighted as one of the most relevant. TB dynamics depends on age in multiple ways, some of which are traditionally simplified in the literature. That is the case of the heterogeneities in contact intensity among different age strata that are common to all airborne diseases, but still typically neglected in the TB case. Furthermore, while demographic structures of many countries are rapidly aging, demographic dynamics are pervasively ignored when modeling TB spreading. In this work, we present a TB transmission model that incorporates country-specific demographic prospects and empirical contact data around a data-driven description of TB dynamics. Using our model, we find that the inclusion of demographic dynamics is followed by an increase in the burden levels predicted for the next decades in the areas of the world that are most hit by the disease today. Similarly, we show that considering realistic patterns of contacts among individuals in different age strata reshapes the transmission patterns reproduced by the models, a result with potential implications for the design of age-focused epidemiological interventions.
Sergio Arregui, Dessislava Marinova, Maria Jose Iglesias, Sofia Samper, Carlos Martin, Joaquin Sanz, and Yamir Moreno, “Data-driven model for the assessment of M. Tuberculosis transmission in evolving demographic structures”, Proceedings of the National Academy of Sciences USA 115, E3238-E3245 (2018).
Disease Localization in Multilayer Networks.
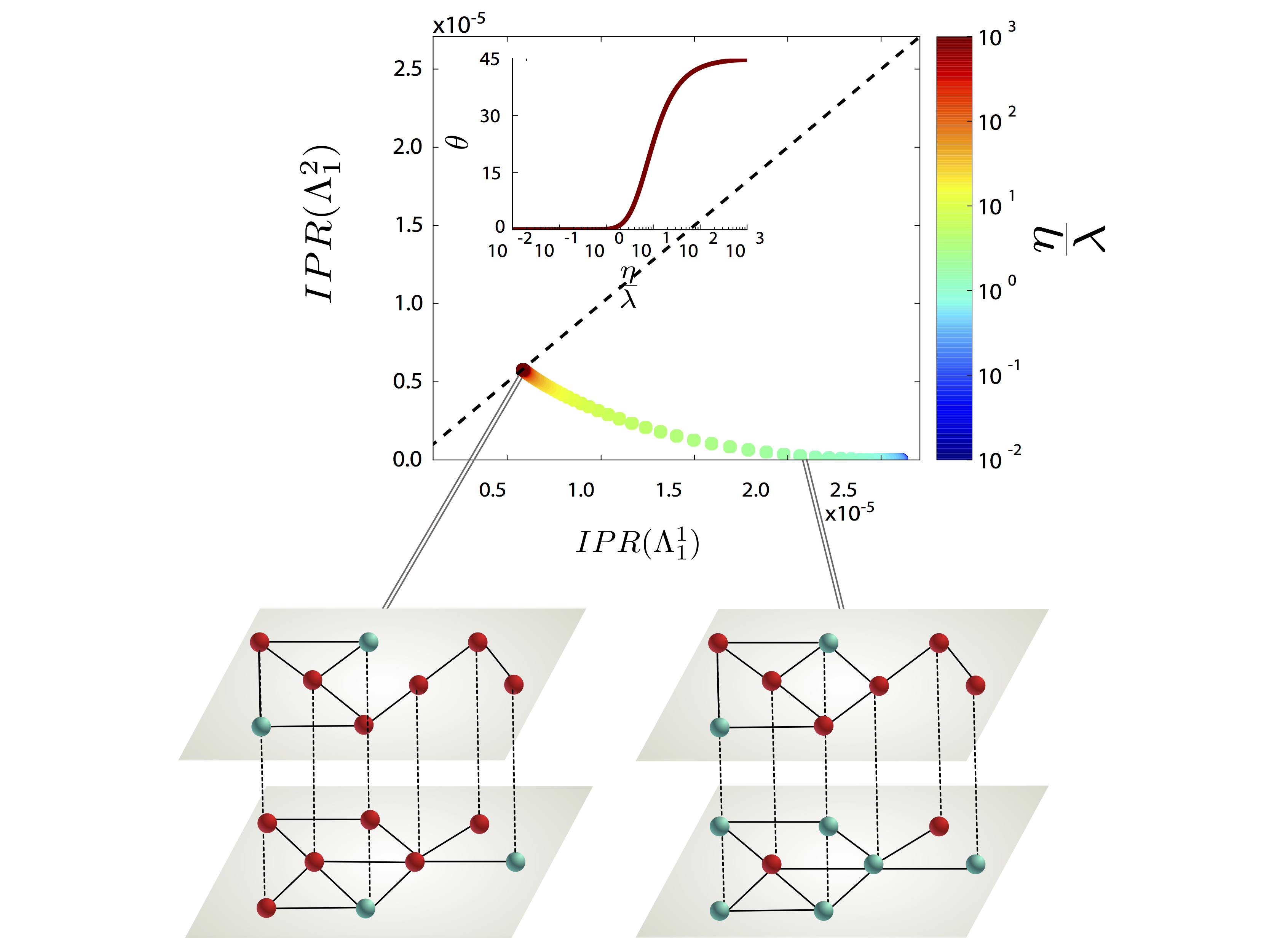
G. Ferraz de Arruda, E. Cozzo, T. P. Peixoto, F. A. Rodrigues, and Y. Moreno, “Disease Localization in Multilayer Networks”, Physical Review X 7, 011014 (2017).
Current modeling of infectious diseases allows for the study of complex and realistic scenarios that go from the population to the individual level of description.
The description of the evolution of a single disease on a particular network of contacts has been the subject of intense research during the last several years. Nowadays, we have a set of tools that allows addressing the previous challenge to a large degree of details. However, in many situations, multiple pathogens coexist within the same host population and usually interact among each other. This includes, for example, systems of competing pathogens (e.g., seasonal influenza) or the so-called syndemic systems (e.g. HIV and Tuberculosis), i.e., two pathogens each of which enhances or impairs the spreading of the other.
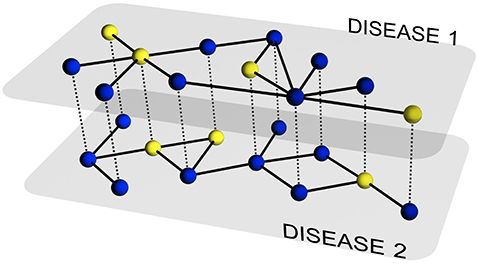
In this paper, we develop a theoretical and computational framework to study the dynamics of concurrent diseases. We propose a model for the description of the simultaneous spreading of two interacting pathogens on the same host population through independent contact networks. The model is based on an heterogenous mean-field approach to describe the critical properties of the dynamics as well as an adequate framework for the temporal description of coupled out of equilibrium outbreaks for both the Susceptible-Infected-Susceptible and Susceptible-Infected-Removed scenarios. The proposed framework allows to analytically derive the epidemic thresholds of the diseases modeled, explicitly addressing the influence on each threshold on aspects such as the prevalence of the conjugate disease, the system size, the architecture of the networks of contacts and the appearance of eventual correlations between them. Overall, our findings provide deep insights into what are the key mechanisms that drive the evolution of interacting diseases and secondly, they pave the way for the development of quantitative, data-driven models for the detailed characterization of concurrent and interacting diseases.
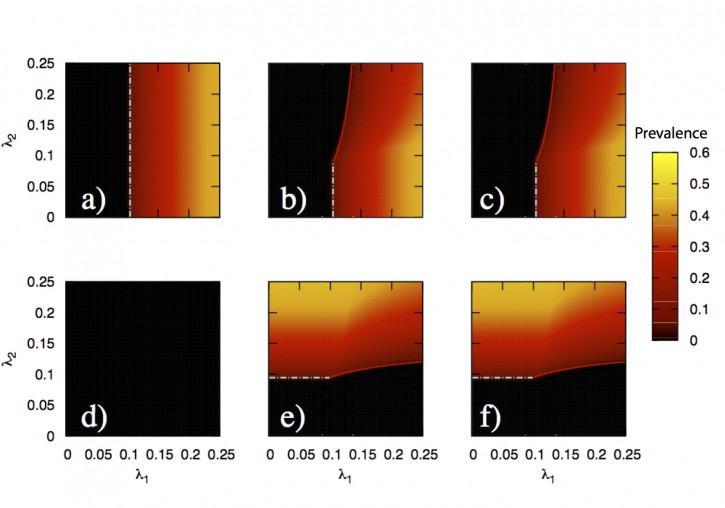
J. Sanz, C.-Y. Xia, S. Meloni and Y. Moreno, “Dynamics of interacting diseases”, Physical Review X 4, 041005 (2014).
The inclusion of mobility processes is a key ingredient in the modeling of the geographic spread of epidemics. Models that explicitly take into account the mobility patterns of individuals range from relatively coarse-grained approaches that consider aggregated traveling flows to highly detailed structured meta-population or agent-based models allowing for the description of billions of individuals.
S. Meloni, N. Perra, A. Arenas, S. Gomez, Y. Moreno, and A. Vespignani, “Modeling Human Mobility Responses to the Large-scale Spreading of Infectious Diseases”, Scientific Reports 1, 62 (2011).
Current state-of-the-art epidemiological models incorporating complex patterns of interactions (no matter whether at the level of meta-populations or not) are devised to deal with a single spreading process, i.e., they are not thought to deal with situations in which several strains of the same disease coexist.
C. Poletto, S. Meloni, V. Colizza, Y. Moreno and A. Vespignani, “Host mobility drives pathogen competition in spatially structured populations”, PLoS Computational Biology 9 (8): e1003169 (2013).
C. Poletto, S. Meloni, A. Van Metre, V. Colizza, Y. Moreno and A. Vespignani, “Characterizing two-pathogen competition in spatially structured environments”, Scientific Reports 5:7895 (2015).
The critical properties of an epidemic outbreak in complex networks were first addressed using the heterogeneous mean-field (HMF) prescription. This framework has been proved to be exact in annealed networks, whose nodes’ degrees are sampled from a fixed degree distribution at each step of the dynamics (i.e. its specific connectivity is fixed only in average).

