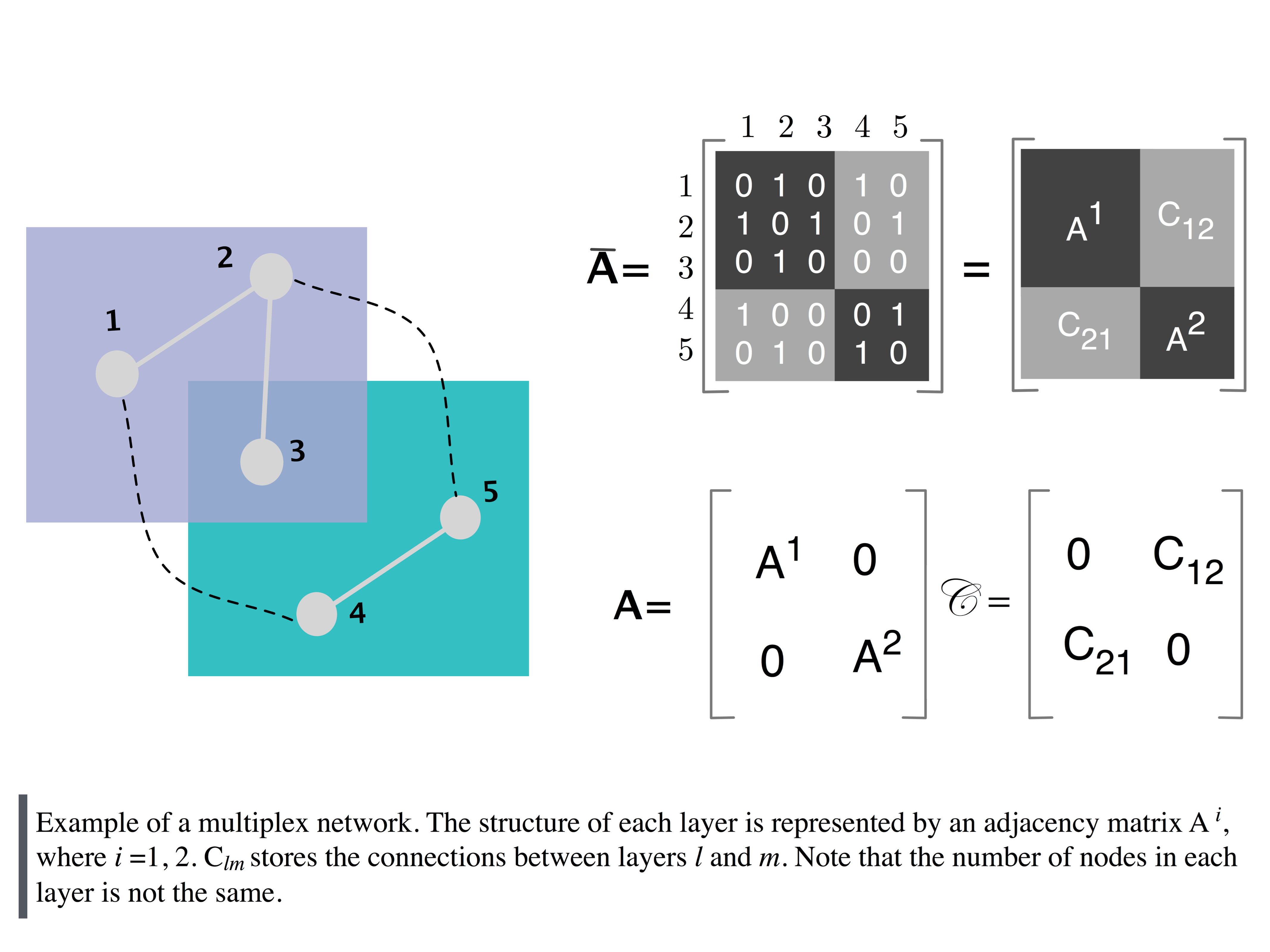
What is a Multilayer Network?
A Multilayer Network -of which Multiplex and Interdependent networks are particular cases- is a network made up by multiple layers, each of which represents a given operation mode, social circle, or temporal instance. This new paradigm in Network Science is believed to be the next step towards a better and full comprehension of modern cyber, social and physical systems such as online social networks, transportation systems, metabolic and regulatory networks, etc. Below, we develop a bit more the need to study these networks and what are the current challenges. We also briefly describe our work in this line of research. To illustrate the potential of this framework, let us first mention one dynamical process that could highly benefit from it: the spreading of one or more diseases or strains on a host population.
Epidemic Spreading in Multilayer Networks.
This is probably one of the most immediate applications of Multilayer Networks. In this case, the new approach allows studying scenarios in which two or more diseases interact cooperatively -i.e., enhancing each other effect- or competitively -i.e., conferring some degree of immunity to the host population in front of the other diseases and thus reducing their impact. As the host population is the same, one can “unfold” its structure and consider that each disease propagates in a layer, hence allowing for different networks of contacts for each of them. The layers are connected by links between the same nodes, as they represent the same individuals of the host population. See our paper below on interacting diseases for more details.
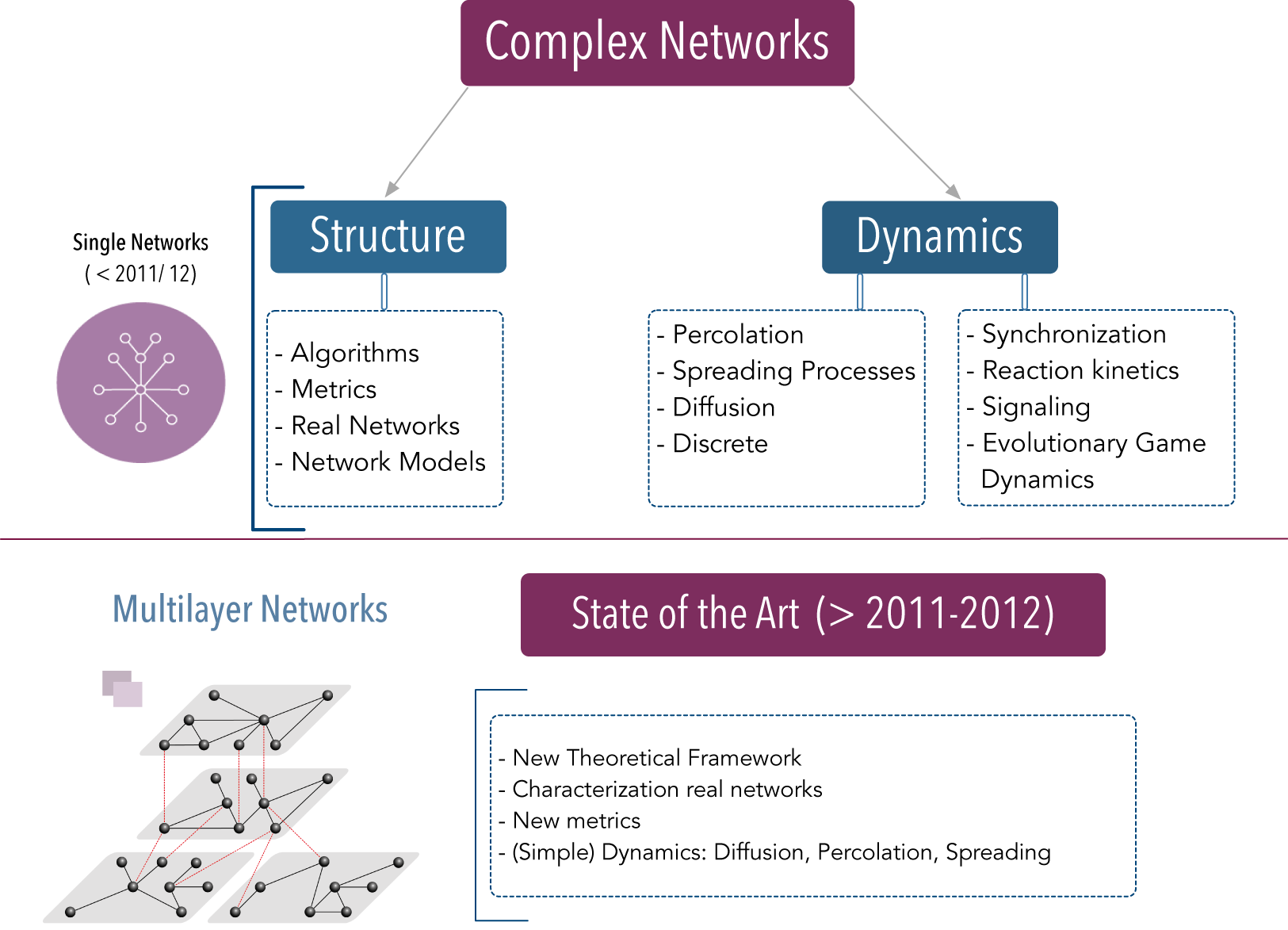Why Multilayer Networks?.The study of Complex Systems in many disciplines through network modeling has allowed us to better understand a myriad of complex phenomena, including the spreading of diseases in modern societies, information dissemination, the functioning of intricate biological pathways and gene circuits, as well as to optimize many manmade systems. By developing a toolbox of metrics, algorithms and theoretical methods, we are closer to tackle many more scientific challenges. However, despite the advances of the last two decades, we also start to see the need of going far beyond where we are if we aim at understanding even more complex phenomena. The reason is very simple: many real-world systems do not operate in isolation. On the contrary, they are interconnected and what happens at a single level of interaction affects the structure and function at another interconnected layer. Examples of the above systems are widespread. Think, for instance, in a social system: a set of nodes represents people that interact among each other. But there are many modes of social interactions between the same people: a single individual has personal, social, professional, etc., circles in the off-line world, but also might have multiple accounts in so-called online social systems (Facebook, Twitter, etc.). The way we have been dealing with this diversity of connections implies that all the aforementioned relations are projected into a single layer, but indeed, not all processes can be simulated on such a simplified aggregated network of contacts. Information diffusion usually takes place through on-line systems, while disease spreading is limited to the set of contacts an individual can physically interact with. As mentioned above, another relevant example is given by how diseases evolve on a particular network of contacts, which has been the subject of intense research during the last several years. Nowadays, we have a set of tools that allows addressing the previous challenge to a large degree of details. However, in many situations, multiple pathogens coexist within the same host population and usually interact among each other. This includes, for example, systems of competing pathogens (e.g., seasonal influenza) or the so-called syndemic systems (e.g. HIV and Tuberculosis), i.e., two pathogens each of which enhances or impairs the spreading of the other. For these latter scenarios, considering multiple networks of contacts or layers is paramount.
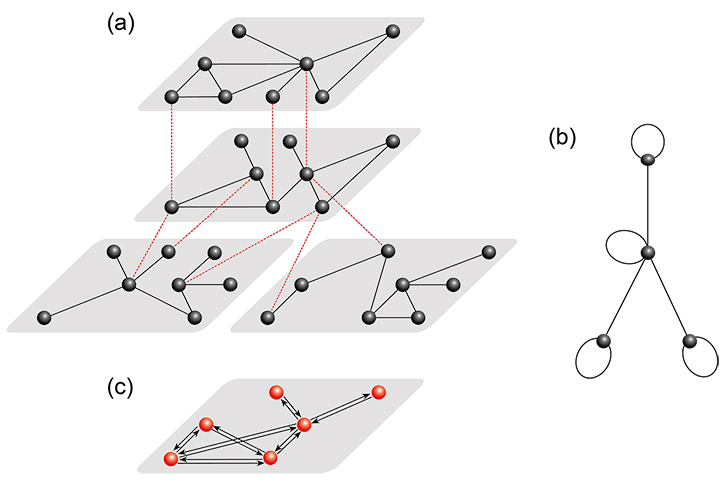Therefore, it is clear that the notion of a “multiplex” network becomes necessary. In a multiplex network, each type of interaction between the nodes is described by a single layer network and the different layers of networks describe the different modes of interaction. Indeed, the scientific interest in multiplex networks has recently seen a surge. However, a fundamental scientific language that can be used consistently and broadly across the many disciplines that are involved in complex systems research has to be developed. This absence is a major obstacle to further progress in this topical area of current interest.
This research line within COSNET is precisely aimed at developing such a language. Our goal is to provide a more sophisticated and general framework that makes it possible to describe both traditional “monoplex” (i.e., single-type links) and multiplex networks. Moreover, as a node from one layer can be linked to another node in any other layer, which leads to “cross talks” between the layers, the dynamics of multilayer systems should also be re-examined. We expect that results coming out from our studies in this area would allow improving our current understanding of the structure and dynamics of natural and manmade complex systems and phenomena.
G. Ferraz de Arruda, E. Cozzo, T. P. Peixoto, F. A. Rodrigues, and Y. Moreno, Physical Review X 7, 011014 (2017).
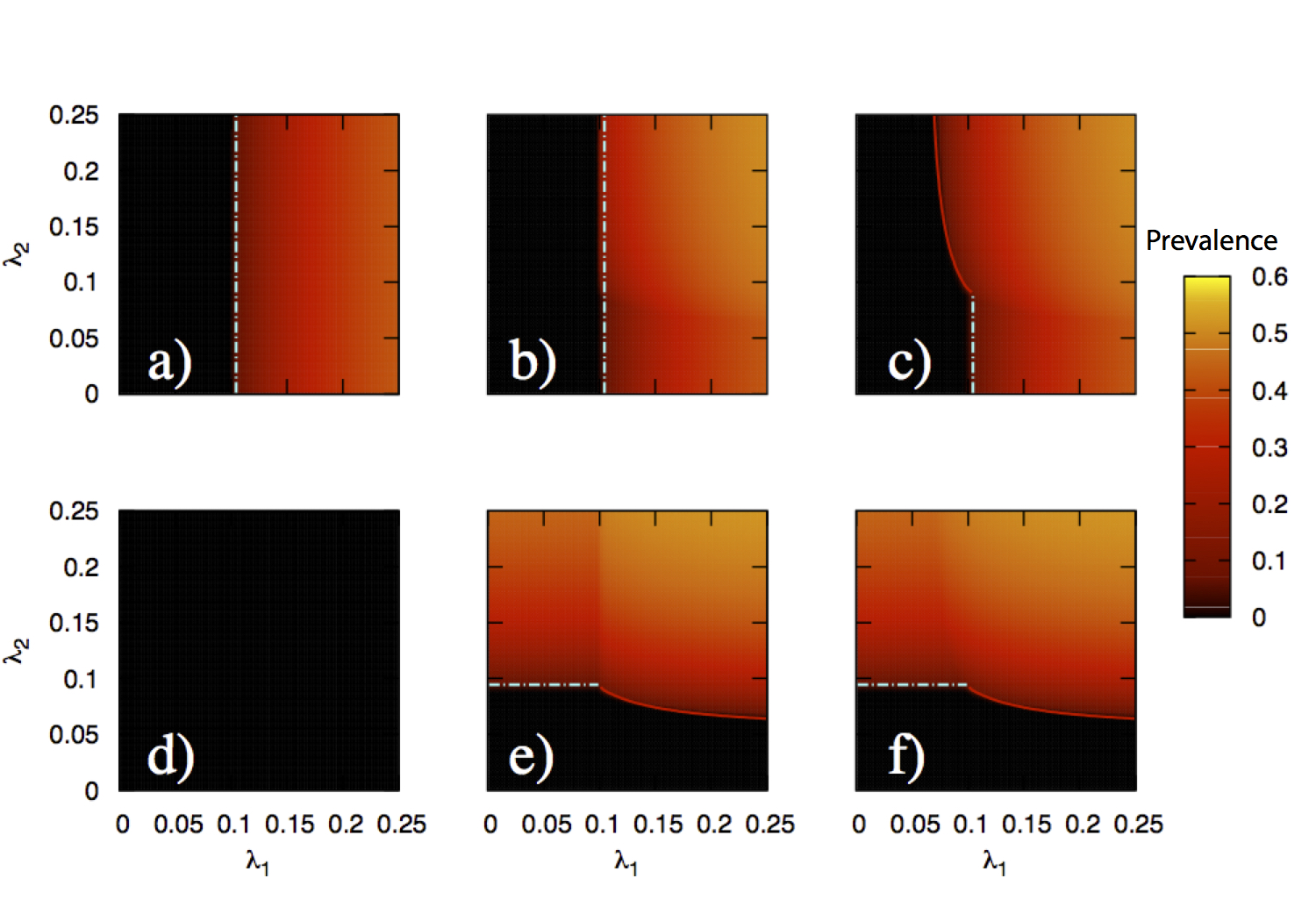
What new insights do we get when the spreading of a disease takes place on a Multilayer Network?: We present a continuous formulation of epidemic spreading on multilayer networks using a tensorial representation, extending the models of monoplex networks to this context. We derive analytical expressions for the epidemic threshold of the susceptible-infected-susceptible (SIS) and susceptible-infected-recovered dynamics, as well as upper and lower bounds for the disease prevalence in the steady state for the SIS scenario. Using the quasistationary state method, we numerically show the existence of disease localization and the emergence of two or more susceptibility peaks, which are characterized analytically and numerically through the inverse participation ratio. At variance with what is observed in single-layer networks, we show that disease localization takes place on the layers and not on the nodes of a given layer. Furthermore, when mapping the critical dynamics to an eigenvalue problem, we observe a characteristic transition in the eigenvalue spectra of the supra-contact tensor as a function of the ratio of two spreading rates: If the rate at which the disease spreads within a layer is comparable to the spreading rate across layers, the individual spectra of each layer merge with the coupling between layers. Finally, we report on an interesting phenomenon, the barrier effect; i.e., for a three-layer configuration, when the layer with the lowest eigenvalue is located at the center of the line, it can effectively act as a barrier to the disease. The formalism introduced here provides a unifying mathematical approach to disease contagion in multiplex systems, opening new possibilities for the study of spreading processes.
Dynamics of interacting diseases.Joaquin Sanz, ChenYi Xia, Sandro Meloni and Yamir Moreno, Physical Review X 4, 041005 (2014).
Does a Multilayer Network representation allow tackling challenges like the interaction of two or more diseases on the same host population?: Current modeling of infectious diseases allows for the study of complex and realistic scenarios that go from the population to the individual level of description. However, most epidemic models assume that the spreading process takes place on a single level (be it a single population, a metapopulation system, or a network of contacts). In particular, interdependent contagion phenomena can be addressed only if we go beyond the scheme-one pathogen-one network. In this paper, we propose a framework that allows us to describe the spreading dynamics of two concurrent diseases. Specifically, we characterize analytically the epidemic thresholds of the two diseases for different scenarios and compute the temporal evolution characterizing the unfolding dynamics. Results show that there are regions of the parameter space in which the onset of a disease’s outbreak is conditioned to the prevalence levels of the other disease. Moreover, we show, for the susceptible-infected-susceptible scheme, that under certain circumstances, finite and not vanishing epidemic thresholds are found even at the limit for scale-free networks. For the susceptible- infected-removed scenario, the phenomenology is richer and additional interdependencies show up. We also find that the secondary thresholds for the susceptible-infected-susceptible and susceptible-infected-removed models are different, which results directly from the interaction between both diseases. Our work thus solves an important problem and paves the way toward a more comprehensive description of the dynamics of interacting diseases.
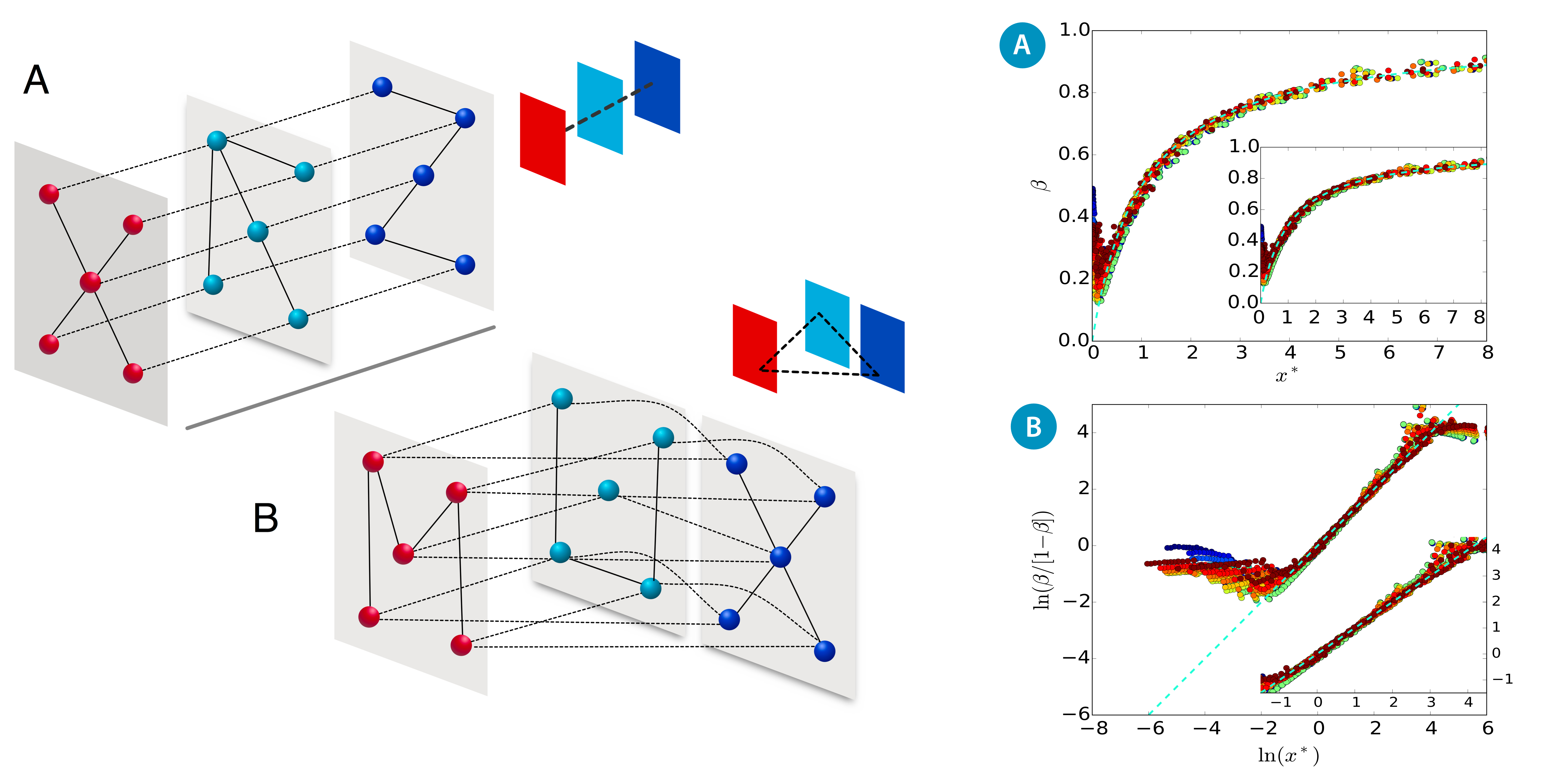
Characterization of multiple topological scales in multiplex networks through supra-Laplacian eigengaps.E. Cozzo and Y. Moreno, Physical Review E 94, 052318 (2016).
Multilayer networks have been the subject of intense research during the past few years, as they represent better the interdependent nature of many real-world systems. Here, we address the question of describing the three different structural phases in which a multiplex network might exist. We show that each phase can be characterized by the presence of gaps in the spectrum of the supra-Laplacian of the multiplex network. We therefore unveil the existence of different topological scales in the system, whose relation characterizes each phase. Moreover, by capitalizing on the coarse-grained representation that is given in terms of quotient graphs, we explain the mechanisms that produce those gaps as well as their dynamical consequences.
A multilayer perspective for the analysis of urban transportation systems.
A. Aleta, S. Meloni, and Y. Moreno, submitted for publication (2017).
Public urban mobility systems are composed by several transportation modes connected together. Most studies in urban mobility and planning often ignore the multi-layer nature of transportation systems considering only aggregated versions of this complex scenario. In this work we present a model for the representation of the transportation system of an entire city as a multiplex network. Using two different perspectives, one in which each line is a layer and one in which lines of the same transportation mode are grouped together, we study the interconnected structure of 9 different cities in Europe raging from small towns to mega-cities like London and Berlin highlighting their vulnerabilities and possible improvements. Finally, for the city of Zaragoza in Spain, we also consider data about service schedule and waiting times, which allow us to create a simple yet realistic model for urban mobility able to reproduce real-world facts and to test for network improvements.
Scaling Properties of Multilayer Random Networks.
J. A. Méndez-Bermúdez, G. Ferraz de Arruda, F. A. Rodrigues, and Y. Moreno, submitted for publication (2017).
Multilayer networks are widespread in natural and manmade systems. Key properties of these networks are their spectral and eigenfunction characteristics, as they determine the critical properties of many dynamics occurring on top of them. In this paper, we numerically demonstrate that the normalized localization length of the eigenfunctions of multilayer random networks follows a simple scaling law. The reported scaling law might help to better understand criticality in multilayer networks as well as to predict the eigenfunction localization properties of them.
Lévy random walks on multiplex networks.
Q. Guo, E. Cozzo, Z. Zheng, and Y. Moreno, Scientific Reports 6:37641 (2016).
Random walks constitute a fundamental mechanism for many dynamics taking place on complex networks. Besides, as a more realistic description of our society, multiplex networks have been receiving a growing interest, as well as the dynamical processes that occur on top of them. Here, inspired by one specific model of random walks that seems to be ubiquitous across many scientific fields, the Lévy flight, we study a new navigation strategy on top of multiplex networks. Capitalizing on spectral graph and stochastic matrix theories, we derive analytical expressions for the mean first passage time and the average time to reach a node on these networks. Moreover, we also explore the efficiency of Lévy random walks, which we found to be very different as compared to the single layer scenario, accounting for the structure and dynamics inherent to the multiplex network. Finally, by comparing with some other important random walk processes defined on multiplex networks, we find that in some region of the parameters, a Lévy random walk is the most efficient strategy. Our results give us a deeper understanding of Lévy random walks and show the importance of considering the topological structure of multiplex networks when trying to find efficient navigation strategies.
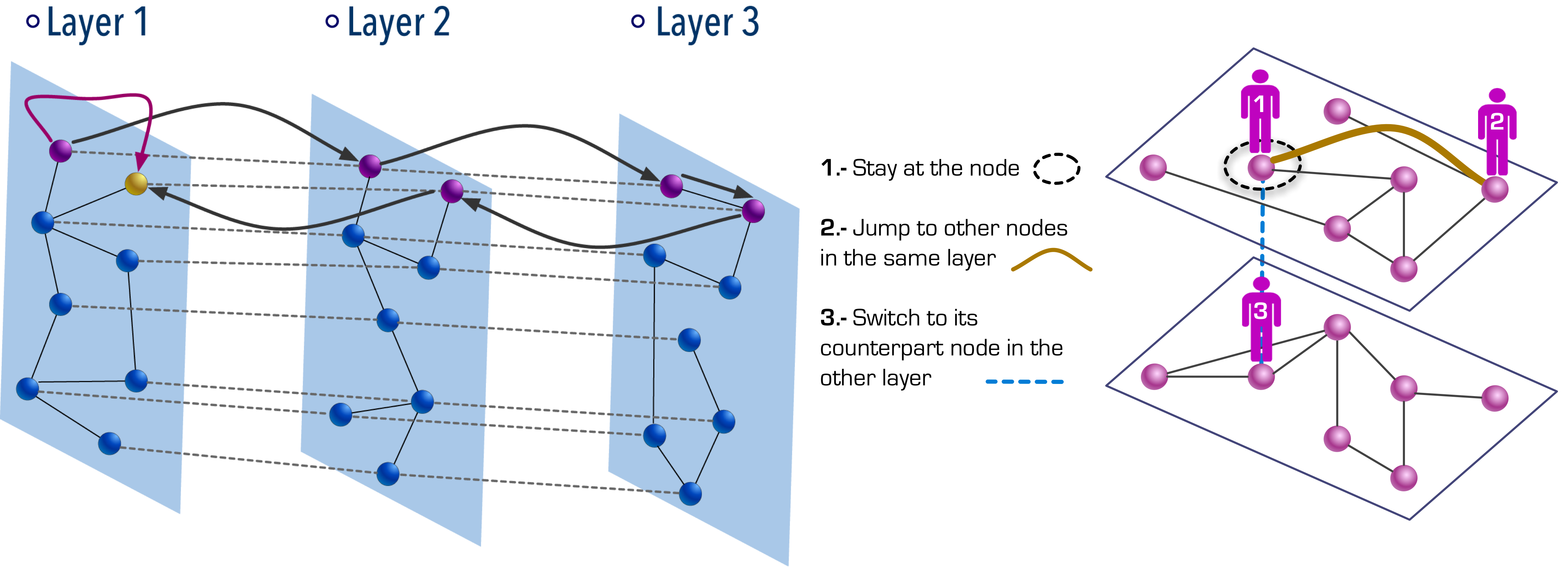
On degree-degree correlations in multilayer networks.
G. Ferraz de Arruda, E. Cozzo, Y. Moreno, and F. A. Rodrigues, Physica D 323-324, 5 (2016).
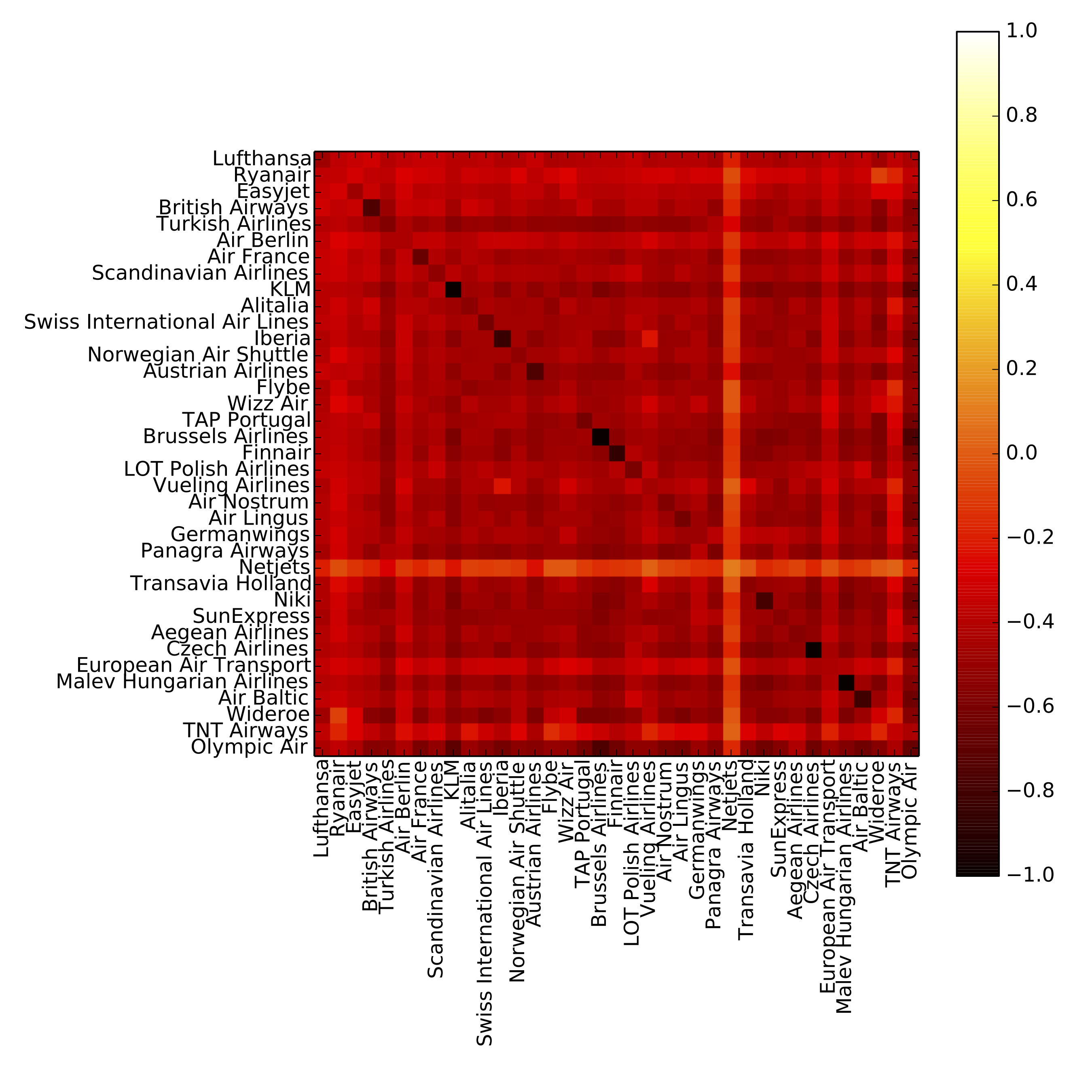
We propose a generalization of the concept of assortativity based on the tensorial representation of multilayer networks, covering the definitions given in terms of Pearson and Spearman coefficients. Our approach can also be applied to weighted networks and provides information about correlations considering pairs of layers. By analyzing the multilayer representation of the airport transportation network, we show that contrasting results are obtained when the layers are analyzed independently or as an interconnected system. Finally, we study the impact of the level of assortativity and heterogeneity between layers on the spreading of diseases. Our results highlight the need of studying degree–degree correlations on multilayer systems, instead of on aggregated networks.
Multilayer networks: metrics and spectral properties.
E. Cozzo, G. Ferraz de Arruda, F. A. Rodrigues, and Y. Moreno, Chapter contribution to the book “Interconnected networks”, edited by F. Schweitzer and A. Garas. ISBN 978-3-319-23947-7, Springer (2016).
Multilayer networks represent systems in which there are several topological levels each one representing one kind of interaction or interdependency between the systems’ elements. These networks have attracted a lot of attention recently be- cause their study allows considering different dynamical modes concurrently. Here, we revise the main concepts and tools developed up to date. Specifically, we focus on several metrics for multilayer network characterization as well as on the spectral properties of the system, which ultimately enable for the dynamical characterization of several critical phenomena. The theoretical framework is also applied for description of real-world multilayer systems.
